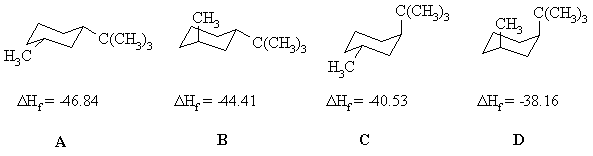
Here is a diagram showing the four isomeric 1-tert-butyl-3-methylcyclohexanes and the DH_f data:

The ΔH_f values are assigned on the basis of stability.  The more stable the isomer, the more exothermic the ΔH_f. (see diagram below if that troubles you). In order to determine the stability order, we need to look at the positions of the two substituents.  Equatorial substitutents are prefered over axial substituents due to the presence of the destabilising 1,3-diaxial interactions (a steric effect) when the substituent is axial due to its proximity to the other axial positions on the same face of the cyclohgexane. The larger the substituent, the more destabilising this steric effect is. So the most stable isomer will be the one with both Me and tBu equatorial, then the one with the larger tBu equatorial and Me axial, then equatorial Me, axial tBu, and the both axial isomer will be the least stable.

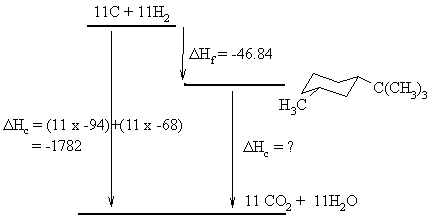
The ΔH_c of the most stable isomer can be calculated using the Hess's Law relationship for the balanced reactions shown to the left.  From the diagram we get the relationship that:

ΔH_c (elements) =  ΔH_f (isomer) +  ΔH_c (isomer).

So, based on the molecular formula we can insert the numbers to get : -1782 = -46.84 + ΔHc,  therefore ΔHc = -1735.16 kcal/mol.
 
 

 
To calculate the equilibrium constant, we need to use the equation ΔG = -RT ln K.
In order to use this we need to approximate ΔG = -46.84--38.16 = -8.68 kcal/mol (for the two cis isomers).
Thus inserting the values,  -8680 cal/mol = -(1.987 cal/molK) (298 K) ln K, so K = 2.3 x 10⁶