| Chapter 13: Spectroscopy |
| Chapter 13: Spectroscopy |
Coupling in H-NMR
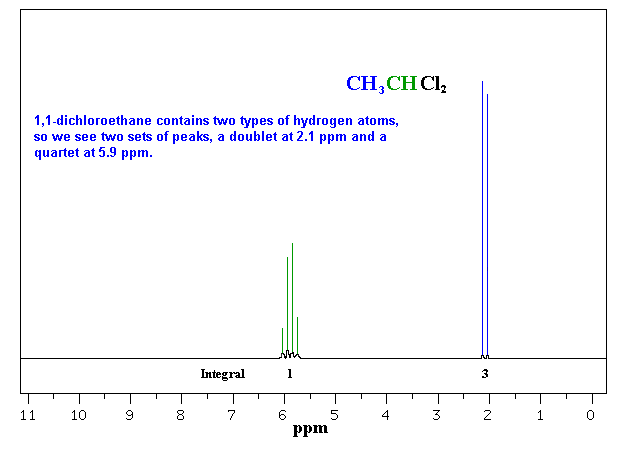
So far the H-NMR spectra that we have looked at have all had different types of protons that are seen as singlets in the spectra. This is not the normal case.... spectra usually have peaks that appear as groups of peaks due to coupling with neighbouring protons, for example, see the spectra of 1,1-dichloroethane shown below.
Coupling arises because the magnetic field of vicinal (adjacent) protons influences the field that the proton experiences.
| To understand the implications of this we should first consider the effect the -CH group has on the adjacent -CH3. | |
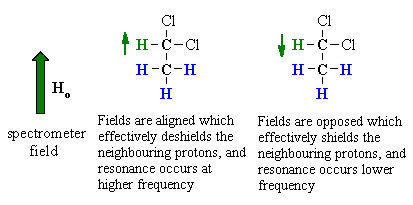 |
The methine -CH can adopt two alignments with respect to the applied field. As a result, the signal for the adjacent methyl -CH3 is split in two lines, of equal intensity, a doublet. |
| Now consider the effect of the -CH3 group has on the adjacent -CH . | |
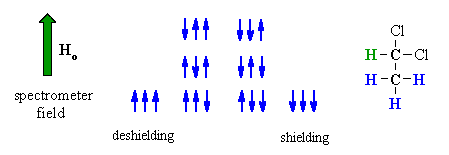 |
The methyl -CH3 protons give rise to 8 possible combinations with respect to the applied field. However, some combinations are equivalent and there are four magnetically different effects. As a result, the signal for the adjacent methine -CH is split into four lines, of intensity ratio 1:3:3:1, a quartet. |
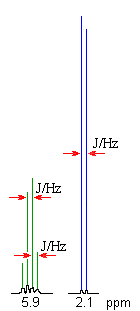 |
The coupling constant, J (usually in frequency units, Hz) is a measure
of the interaction between a pair of protons. In a vicinal system of the general type, Ha-C-C-Hb then the coupling of Ha with Hb, Jab, MUST BE EQUAL to the coupling of Hb with Ha, Jba, therefore Jab = Jba. The implications are that the spacing between the lines in the coupling patterns are the same as can be seen in the coupling patterns from the H-NMR spectra of 1,1-dichloroethane (see left). |
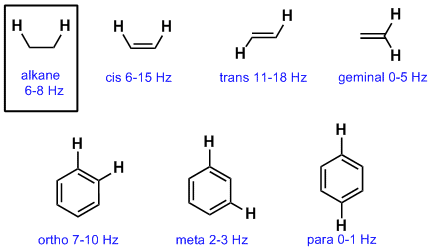
Typical Coupling Constants
So far we have emphasised vicinal coupling of H atoms on adjacent sp3 C atoms. This coupling constant is typically about 6-8 Hz. Coupling is controlled by geometry and the orbitals involved between the coupling nuclei and therefore other types of systems have slightly different coupling constants as shown below:
Notes:
Pascal's Triangle
| The relative intensitites of the lines in a coupling pattern is given
by a binomial expansion or more conviently by Pascal's triangle.
To derive Pascal's triangle, start at the apex, and generate each lower row by creating each number by adding the two numbers above and to either side in the row above together. The first six rows are shown to the right. So for H-NMR a proton with zero neighbours, n = 0, appears as a single line, a proton with one neighbours, n =1 as two lines of equal intensity, a proton with two neighbours, n = 2, as three lines of intensities 1 : 2 : 1, etc. |
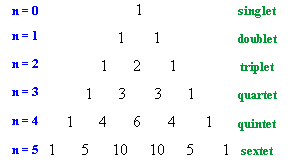 |
Summary
| © Dr. Ian Hunt, Department of Chemistry |