|
|
|
|
Conformational Analysis Answers
| Ans 1: |
First, as in any question you encounter with a compound name,
draw out the compound (hence understanding nomenclature is vital). Using
your model kit will also help solving this problem. It is convienient to
describe the C3-C4 bond system as having a C3- and C4-methyl groups and
a C3-t-butyl. In general terms, all the energy maxima will be eclipsed conformations, and the minima will be staggered. The highest energy conformation will be with the C3-t-butyl and C4-methyl groups eclipsed, B. Rotation will move to the least stable of the staggered conformers with the C4-methyl group gauche to both the C3-t-butyl and methyl groups, A. Further rotation gives the eclipsed conformer with the C3- and C4- methyls eclipsed, E, then onto the lowest energy conformation will be with these same two groups at 180o to each other, in the staggered conformation, D. Now to the most favourable eclipsed conformer with each of the R groups eclipsed only by H atoms, AB. The next staggered conformation has the C3-t-butyl group gauche to the C4-methyl group, C, and finally back to B. |
| Ans 2:
|
The four structures are shown below along with their respective ΔHf
values. The most stable conformation will have the most exothermic
ΔHf and this will correspond to the situation with both alkyl
groups in the more favourable equatorial position. Equatorial substitutents
are prefered over axial substituents due to the presence of the destabilising
1,3-diaxial interactions (a steric effect) when the substituent is axial
due to its proximity to the other axial positions on the same face of the
cyclohexane. The larger the substituent, the more destabilising this steric
effect is. So the most stable isomer will be the one with both Me and tBu
equatorial, then the one with the larger tBu equatorial and Me axial, then
equatorial Me, axial tBu, and the both axial isomer will be the least stable.
To calculate the equilibrium constant, we need to use the equation ΔG
= -RT ln K and make the approximation |
||||||||||||||||||||||
| Ans 3:
|
Here is a diagram showing the reactions and the data provided in the question:
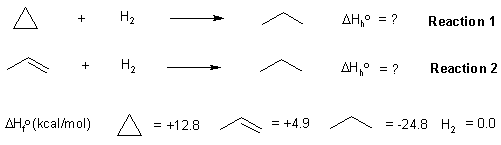
The heat of a reaction (in this case the heat of hydrogenation) can be calculated from the heats of formation of the products and starting materials (also see the figure below):
With this data, we can create the required energy diagram. If a C=C is
146 kcal/mol and a C-C is 83 kcal/mol, then we can estimate the strength
of a π bond as 146 - 83 = 63 kcal/mol. This means a σ bond is 20 kcal/mol
stonger than a π bond. If we correct for the differing bonds, then the heat of hydrogenation
of cyclopropane becomes -57.6 kcal/mol. (ie. more exothermic by 20 kcal/mol)
|
 |
© Dr. Ian Hunt, Department of Chemistry |